Solving Wordle with Z3: A Case Study
Jeff Baranski
03/13/2022
Source Code
Abstract
A case study where we show how to use the Z3 SMT solver to simulate and solve Wordle puzzles. First we will explain what Wordle is, how to play the game, what Z3 is, and what SMT is. Next we will describe how to transcribe the rules of Wordle into a mathematical formula that can be leveraged by the Z3 SMT solver. Then we will explain various Wordle solving strategies we want Z3 to simulate (we want to determine if any single strategy can consistently solve the puzzles with the least amount of guesses over the entire Wordle answer set). Finally we present the results of the simulations.
What is Wordle?
Wordle [1] is a simple word guessing game. You have six tries to guess a secret five letter word. Each letter sits in a tile. After each guess, the color of the tiles will change to show how close your guess was to the answer. A green tile means the letter is in the correct spot. A yellow tile means the letter is in the answer but in the wrong spot. A gray tile means the letter is not in the answer.
Let’s take a look at a simple example:

- After the first guess CHIDE, we know there is an E in the answer somewhere (and E won’t be the last letter in the answer). The answer does not contain C, H, I, D.
- After the second guess SEALS, we know the answer starts with an S. We know there is an E in the answer somewhere (and E is not the second or the last letter in the answer). The answer does not contain A, L. The answer does not contain a second S.
- After the third guess SWEEP, we know the first four letters in the answer are S, W, E, E. The answer does not contain P.
- We guess correctly on the fourth guess (with two guesses to spare), SWEET.
NOTE: There are 2309 words listed as valid answers. There are 10638 words listed as valid guesses (that are not ever going to be answers). The game will not allow us to make silly guesses, like AAAAA, BBBBB, ABCDEF, etc…
NOTE: I pulled the answers list and valid guesses list from the New York Times version of the game circa February 1st, 2022. Any changes in the answer list or the valid guesses list since then is not accounted for in this analysis.
What is Z3?
“Z3 is a theorem prover from Microsoft Research” [2].
What is satisfiability modulo theories (SMT)?
“In computer science and mathematical logic, satisfiability modulo theories (SMT) is the problem of determining whether a mathematical formula is satisfiable” [3].
Let’s take a look at a simple example:
- Consider the following constraint {x ∈ ℤ | 0 ≤ x ≤ 10}. Z3 will find it to be satisfiable. If we ask Z3 for a model, it will provide us with a number between 0 and 10.
- Python program where Z3 solves the constraint {x ∈ ℤ | 0 ≤ x ≤ 10}.
import z3
x = z3.Int('x')
solver = z3.Solver()
solver.add(z3.And(x >= 0, x <= 10))
print(solver.check())
print(solver.model())
sat
[x = 10]
- Z3 found a solution, x = 10. It was able to prove that the formula is satisfiable given the constraints.
Let’s take a look at another simple example:
- Consider the following constraint {x ∈ ℤ | 0 ≤ x ≤ 10}, x ∉ {1, 4, 8, 9}. Z3 will find it to be satisfiable. If we ask Z3 for a model, it will provide us with a number between 0 and 10 that is not the numbers 1, 4, 8, 9.
- Python program where Z3 solves the constraint {x ∈ ℤ | 0 ≤ x ≤ 10}, x ∉ {1, 4, 8, 9}.
import z3
x = z3.Int('x')
solver = z3.Solver()
solver.add(z3.And(x >= 0, x <= 10))
solver.add(z3.And(x != 1, x != 4, x != 8, x != 9))
print(solver.check())
print(solver.model())
sat
[x = 0]
- Z3 found a solution, x = 0. It was able to prove that the formula is satisfiable given the constraints.
Wordle rules transcribed to a mathematical formula
The Wordle rules can be transcribed to a mathematical formula via a set of logical expressions and logical constraints, similar to but slightly more complex than the simple examples provided in the What is satisfiability modulo theories (SMT)? section above.
Z3 will be able to generate Wordle guesses based on the constraints we add to it from the transcribed rules. As Z3 makes guesses, the constraints on the problem will expand (and thus the set of available answers will narrow), until Z3 is able to guess the right answer.
How to transcribe the Wordle rules to a mathematical formula:
- First we take each letter in the English alphabet and map it to an integer: a: 0, b: 1, c: 2, d: 3, e: 4, f: 5, g: 6, h: 7, i: 8, j: 9, k: 10, l: 11, m: 12, n: 13, o: 14, p: 15, q: 16, r: 17, s: 18, t: 19, u: 20, v: 21, w: 22, x: 23, y: 24, z: 25.
- Create a separate variable for each letter in a five letter answer: letter1, letter2, letter3, letter4, letter5.
- Combine the answers list and valid guesses list into a new total list (will be referred to as total list from here on out).
- For each word in the total list, take each separate letter and map it to its integer equivalent. For example: S, W, E, E, T will become 18, 22, 4, 4, 19.
- Create a conjunction of these integer values using the answer letter variables. For example: (letter1 = 18 ∧ letter2 = 22 ∧ letter3 = 4 ∧ letter4 = 4 ∧ letter5 = 19).
- After we create a conjunction of integer values for each word in the total list, create a disjunction of each. For example: (letter1 = 18 ∧ letter2 = 22 ∧ letter3 = 4 ∧ letter4 = 4 ∧ letter5 = 19) ∨ (letter1 = 18 ∧ letter2 = 22 ∧ letter3 = 4 ∧ letter4 = 4 ∧ letter5 = 15) ∨ etc… This basically says: The answer is S, W, E, E, T or the answer is S, W, E, E, P or the answer is… and so on.
- Z3 equivalent syntax:
solver.add(z3.Or([z3.And([letter1 == 18, letter2 == 22, letter3 == 4, letter4 == 4, letter5 == 19]), z3.And([letter1 == 18, letter2 == 22, letter3 == 4, letter4 == 4, letter5 == 19)], etc...)
The steps we just described above is the first constraint we add to Z3. Z3 is now able to provide us with a first guess. Let's pretend the answer is S, W, E, E, T (18, 22, 4, 4, 19) and the first guess from Z3 is C, H, I, D, E (2, 7, 8, 3, 4).
- We know there is an E (4) in the answer somewhere (and E (4) won’t be the last letter in the answer). The answer does not contain C, H, I, D (2, 7, 8, 3).
- We create constraints to add to Z3 based on the feedback from the incorrect guess: letter5 ≠ 4 ∧ (letter1 = 4 ∨ letter2 = 4 ∨ letter3 = 4 ∨ letter4 = 4) ∧ letter1 ≠ 2 ∧ letter2 ≠ 2 ∧ letter3 ≠ 2 ∧ letter4 ≠ 2 ∧ letter5 ≠ 2 ∧ letter1 ≠ 7 ∧ letter2 ≠ 7 ∧ letter3 ≠ 7 ∧ letter4 ≠ 7 ∧ letter5 ≠ 7 ∧ letter1 ≠ 8 ∧ letter2 ≠ 8 ∧ letter3 ≠ 8 ∧ letter4 ≠ 8 ∧ letter5 ≠ 8 ∧ letter1 ≠ 3 ∧ letter2 ≠ 3 ∧ letter3 ≠ 3 ∧ letter4 ≠ 3 ∧ letter5 ≠ 3.
- Z3 equivalent syntax:
solver.add(letter5 != 4)
solver.add(z3.Or([letter1 == 4, letter2 == 4, letter3 == 4, letter4 == 4]))
solver.add(letter1 != 2)
solver.add(letter2 != 2)
solver.add(letter3 != 2)
solver.add(letter4 != 2)
solver.add(letter5 != 2)
solver.add(letter1 != 7)
solver.add(letter2 != 7)
solver.add(letter3 != 7)
solver.add(letter4 != 7)
solver.add(letter5 != 7)
solver.add(letter1 != 8)
solver.add(letter2 != 8)
solver.add(letter3 != 8)
solver.add(letter4 != 8)
solver.add(letter5 != 8)
solver.add(letter1 != 3)
solver.add(letter2 != 3)
solver.add(letter3 != 3)
solver.add(letter4 != 3)
solver.add(letter5 != 3)
With the new constraints added to Z3, we are ready to receive a second guess. Let’s pretend the second guess from Z3 is S, E, A, L, S (18, 4, 0, 11, 18).
- We know the answer starts with an S (18). We know there is an E (4) in the answer somewhere (and E (4) is not the second letter in the answer). The answer does not contain A, L (0, 11). The answer does not contain a second S (18).
- We create constraints to add to Z3 based on the feedback from the incorrect guess: letter1 = 18 ∧ letter2 ≠ 4 ∧ (letter1 = 4 ∨ letter3 = 4 ∨ letter4 = 4) ∧ letter1 ≠ 0 ∧ letter2 ≠ 0 ∧ letter3 ≠ 0 ∧ letter4 ≠ 0 ∧ letter5 ≠ 0 ∧ letter1 ≠ 11 ∧ letter2 ≠ 11 ∧ letter3 ≠ 11 ∧ letter4 ≠ 11 ∧ letter5 ≠ 11 ∧ |{letter1 = 18, letter2 = 18, letter3 = 18, letter4 = 18, letter5 = 18}| = 1.
- Z3 equivalent syntax:
solver.add(letter 1 == 18)
solver.add(letter2 != 4)
solver.add(z3.Or([letter1 == 4, letter3 == 4, letter4 == 4]))
solver.add(letter1 != 0)
solver.add(letter2 != 0)
solver.add(letter3 != 0)
solver.add(letter4 != 0)
solver.add(letter5 != 0)
solver.add(letter1 != 11)
solver.add(letter2 != 11)
solver.add(letter3 != 11)
solver.add(letter4 != 11)
solver.add(letter5 != 11)
solver.add(z3.AtMost(letter1 == 18, letter2 == 18, letter3 == 18, letter4 == 18, letter5 == 18, 1)
After the second guess constraints are added to Z3, we are ready to receive a third guess. Let’s pretend the third guess from Z3 is S, W, E, E, P (18, 22, 4, 4, 15).
- We already accounted for the answer starting with an S (18). We now know the second letter starts with a W (22), the third letter starts with an E (4), and the fourth letter starts with an E (4). The answer does not contain a P (15).
- We create constraints to add to Z3 based on the feedback from the incorrect guess: letter2 = 22 ∧ letter3 = 4 ∧ letter4 = 4 ∧ letter1 ≠ 15 ∧ letter2 ≠ 15 ∧ letter3 ≠ 15 ∧ letter4 ≠ 15 ∧ letter5 ≠ 15.
- Z3 equivalent syntax:
solver.add(letter2 == 22)
solver.add(letter3 == 4)
solver.add(letter4 == 4)
solver.add(letter1 != 15)
solver.add(letter2 != 15)
solver.add(letter3 != 15)
solver.add(letter4 != 15)
solver.add(letter5 != 15)
After the third guess constraints are added to Z3, we are ready to receive a fourth guess. Let’s pretend the fourth guess from Z3 is S, W, E, E, T (18, 22, 4, 4, 19). This matches the correct answer. Z3 took four guesses to solve this Wordle puzzle.
NOTE: typon’s [4] Z3 Wordle article is very informative. Some of the ideas in this section are based on the basic concepts explained in that article.
Wordle solving strategies
These are the Wordle solving strategies we ran simulations on:
NOTE: Simulation means we solved all 2309 Wordle answers available in the answers list with a given strategy.
NOTE: The transcribed rules described in the Wordle rules transcribed to a mathematical formula section will be referred to as the base rules in this section.
NOTE: I realize I went a little overboard with the sheer number of similar optimize* strategies, but I was curious if any small change to a strategy made a big difference on how well Z3 could solve the Wordle puzzles (spoiler alert: it didn’t).
- Solver (Strategy 01): This strategy involves using the z3.Solver object [5] to solve Wordle puzzles based solely on the base rules.
- Optimize (Strategy 02): This strategy involves using the z3.Optimize object [6][7] to solve Wordle puzzles based solely on the base rules.
- Optimize and prefer words with no duplicate letters (Strategy 03): Extends optimize strategy and adds a soft constraint to prefer words that contain no duplicate letters. This is a MaxSMT problem.
- Optimize, prefer words with no duplicate letters, and prefer words with two or less duplicate letters (Strategy 04): Extends optimize and prefer words with no duplicate letters strategy and adds a soft constraint to prefer words that contain two or less duplicate letters. This is a MaxSMT problem.
- Optimize and prefer words with two or less duplicate letters (Strategy 05): Extends optimize strategy and adds a soft constraint to prefer words that contain two or less duplicate letters. This is a MaxSMT problem.
- Optimize with letter frequency from total list (Strategy 06): Extends optimize strategy and adds soft constraints to prefer words that contain the most frequent letters in total list (so if in total list 90% of the words contain an E somewhere, Z3 will prefer words that contain E’s). This is a MaxSMT problem.
- Optimize with letter frequency from total list and prefer words with no duplicate letters (Strategy 07): Extends optimize with letter frequency from total list strategy and adds a soft constraint to prefer words that contain no duplicate letters (no duplicate letters soft constraint has a higher weight than letter frequency). This is a MaxSMT problem.
- Optimize with letter frequency from total list, prefer words with no duplicate letters, and prefer words with two or less duplicate letters (Strategy 08): Extends optimize with letter frequency from total list and prefer words with no duplicate letters strategy and adds a soft constraint to prefer words that contain two or less duplicate letters. This is a MaxSMT problem.
- Optimize with letter frequency from total list and prefer words with two or less duplicate letters (Strategy 09): Extends optimize with letter frequency from total list strategy and adds a soft constraint to prefer words that contain two or less duplicate letters. This is a MaxSMT problem.
- Optimize with letter frequency from answer list (Strategy 10): Same as optimize with letter frequency from total list strategy except we use the answer list instead of the total list for letter frequencies.
- Optimize with letter frequency from answer list and prefer words with no duplicate letters (Strategy 11): Same as optimize with letter frequency from total list and prefer words with no duplicate letters strategy except we use the answer list instead of the total list for letter frequencies.
- Optimize with letter frequency from answer list , prefer words with no duplicate letters, and prefer words with two or less duplicate letters (Strategy 12): Same as optimize with letter frequency from total list, prefer words with no duplicate letters, and prefer words with two or less duplicate letters strategy except we use the answer list instead of the total list for letter frequencies.
- Optimize with letter frequency from answer list and prefer words with two or less duplicate letters (Strategy 13): Same as optimize with letter frequency from total list and prefer words with two or less duplicate letters strategy except we use the answer list instead of the total list for letter frequencies.
- Optimize with letter position frequency from total list (Strategy 14): Same as Optimize with letter frequency from total list strategy except prefer words with the most frequent letters by letter position (so if in total list letter1 contains E’s 90% of the time, Z3 will prefer words that start with E).
- Optimize with letter position frequency from total list and prefer words with no duplicate letters (Strategy 15): Same as optimize with letter frequency from total list and prefer words with no duplicate letters strategy except prefer words with the most frequent letters by letter position (so if in total list letter1 contains E’s 90% of the time, Z3 will prefer words that start with E).
- Optimize with letter position frequency from total list, prefer words with no duplicate letters, and prefer words with two or less duplicate letters (Strategy 16): Same as optimize with letter frequency from total list, prefer words with no duplicate letters, and prefer words with two or less duplicate letters strategy except prefer words with the most frequent letters by letter position (so if in total list letter1 contains E’s 90% of the time, Z3 will prefer words that start with E).
- Optimize with letter position frequency from total list and prefer words with two or less duplicate letters (Strategy 17): Same as optimize with letter frequency from total list and prefer words with two or less duplicate letters strategy except prefer words with the most frequent letters by letter position (so if in total list letter1 contains E’s 90% of the time, Z3 will prefer words that start with E).
- Optimize with letter position frequency from answer list (Strategy 18): Same as optimize with letter position frequency from total list strategy except we use the answer list instead of the total list for letter frequencies.
- Optimize with letter position frequency from answer list and prefer words with no duplicate letters (Strategy 19): Same as optimize with letter position frequency from total list and prefer words with no duplicate letters strategy except we use the answer list instead of the total list for letter frequencies.
- Optimize with letter position frequency from answer list, prefer words with no duplicate letters, and prefer words with two or less duplicate letters (Strategy 20): Same as optimize with letter position frequency from total list, prefer words with no duplicate letters, and prefer words with two or less duplicate letters strategy except we use the answer list instead of the total list for letter frequencies.
- Optimize with letter position frequency from answer list and prefer words with two or less duplicate letters (Strategy 21): Same as optimize with letter position frequency from total list and prefer words with two or less duplicate letters strategy except we use the answer list instead of the total list for letter frequencies.
- Norvig (Strategy 22): Peter Norvig’s “What is a winning strategy I can memorize” [8]. “Guess the four words HANDY, SWIFT, GLOVE, CRUMP first. For guesses 5 and 6, guess any word consistent with the replies.”
Wordle solving strategy simulations
NOTE: All strategy simulations were run on a system with 32 GB RAM and an Intel® Core™ i7-7700k CPU @ 4.2ghz processor.
NOTE: Simulation means we solved all 2309 Wordle answers available in the answers list with a given strategy.
NOTE: Strategies are labeled as Strategy 01, Strategy 02, etc… on the graphs to keep the labels readable. The strategies are numbered in the order they appear in the Wordle solving strategies section.
All Strategies
Win/Loss % by strategy (win = solved the puzzle with 6 guesses or less)
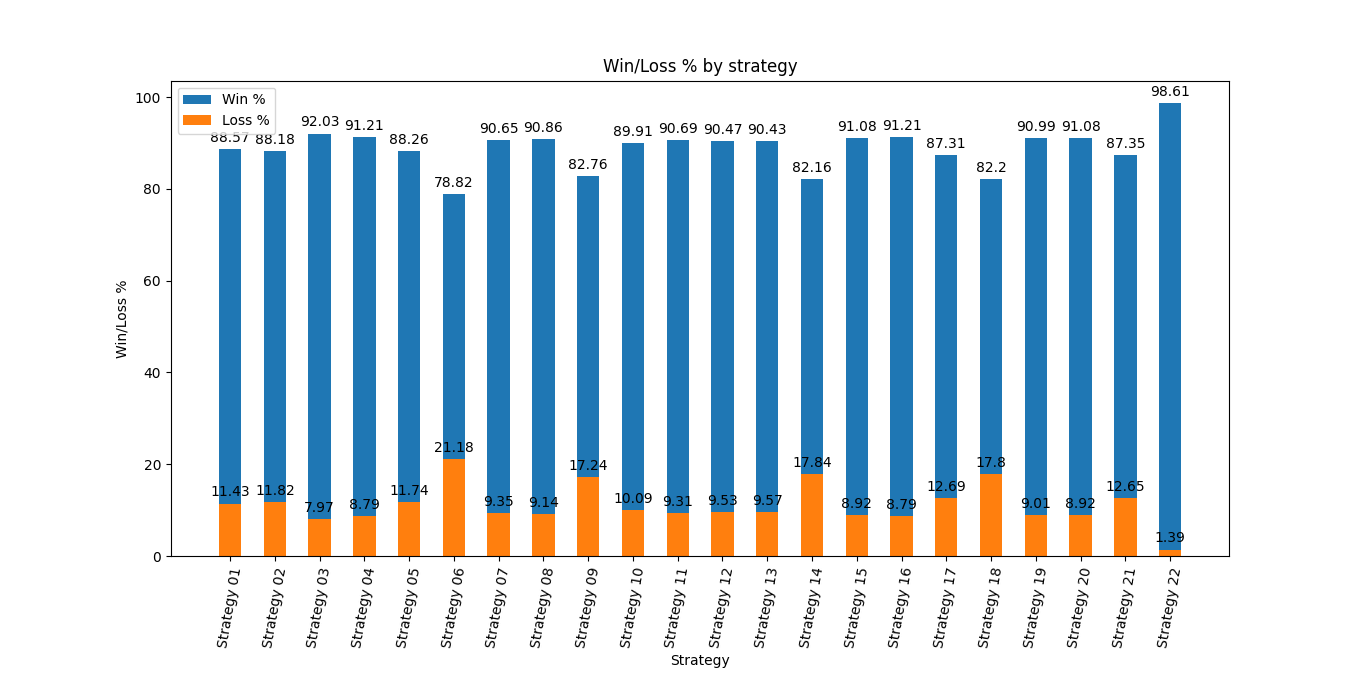
- Norvig (strategy 22) is clearly the best performer.
- I expected the strategies optimize with letter frequency from total list (strategy 06), optimize with letter frequency from answer list (strategy 10), optimize with letter position frequency from total list (strategy 14), and optimize with letter position frequency from answer list (Strategy 18) to all perform sub-optimally. Strategy 10 ended up performing better than the others, which was puzzling. I think if I re-ran the simulations for this strategy enough times, it would converge towards a lower win/loss % like its peers.
- All other strategies performed very well all things considered. An 87% winning percentage for most strategies was much better than I predicted I would get going into this experiment.
Guess count by strategy
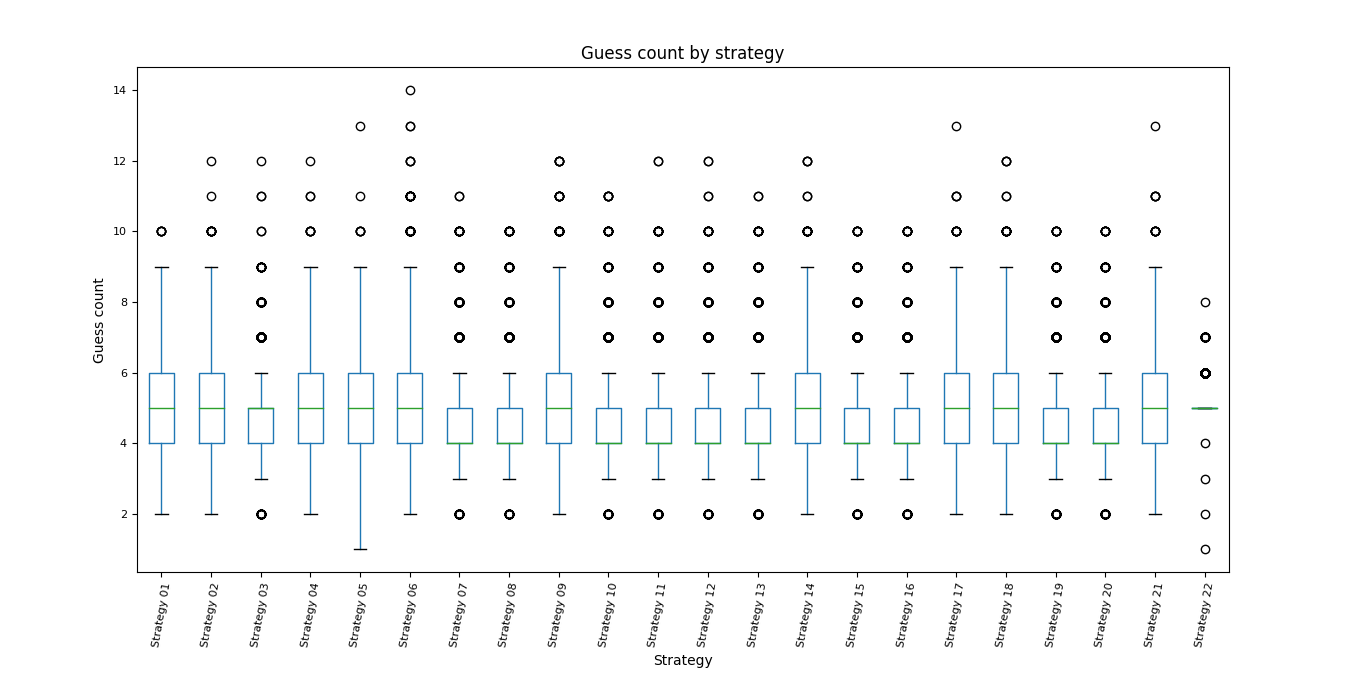
- Unsurprisingly, Norvig (strategy 22) was the best performer here as well.
- The other strategies all performed within a similar level, give or take a few outliers.
Simulation time (hours) by strategy
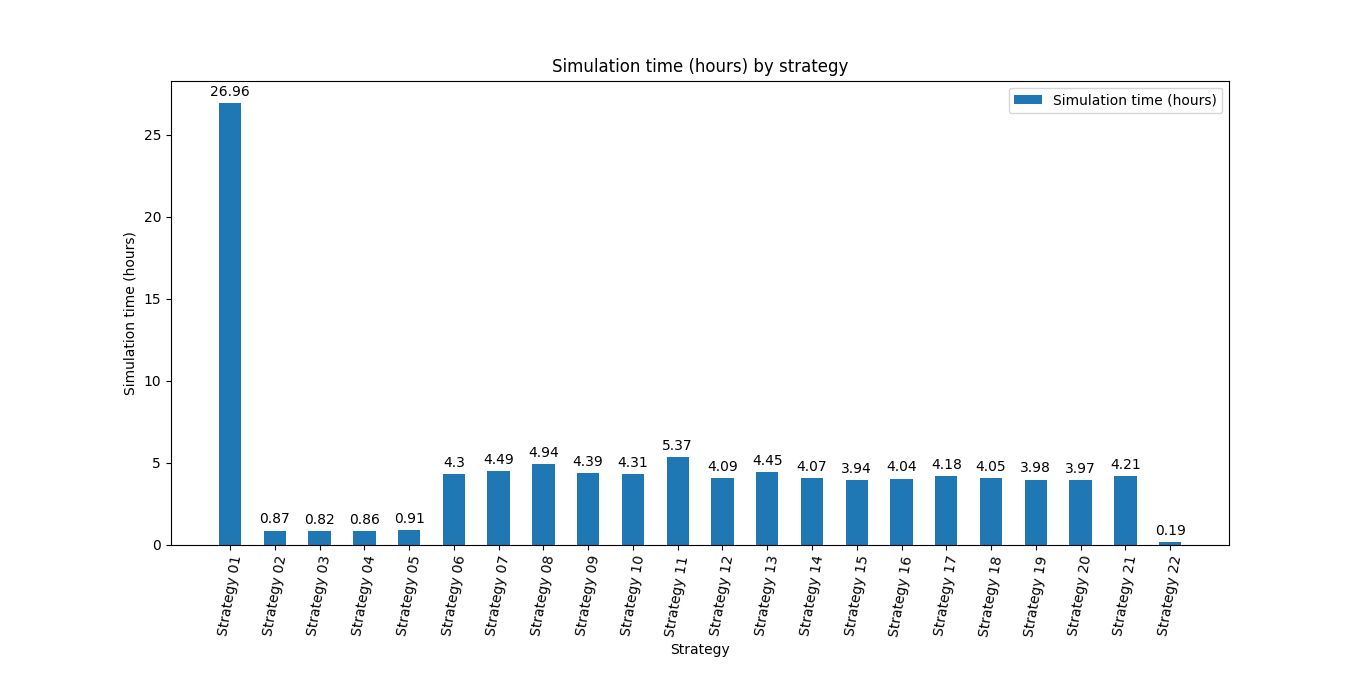
- Norvig (strategy 22) was the best performer here as well. This is because we hardcoded the first four guesses. This sped up the simulation time dramatically. Due to the constraints we gained from the previous hardcoded guesses, Z3 required much less processing power to make a decent next guess.
- Solver (strategy 01) was the worst performer. This strategy used the solver object [5] provided by Z3.
- The rest of the strategies used the optimize object [6][7] from Z3 (except Norvig (strategy 22), which is explained above), which caused extremely impressive performance gains.
- The optimize (strategy 02), optimize and prefer words with no duplicate letters (strategy 03), optimize, prefer words with no duplicate letters, and prefer words with two or less duplicate letters (strategy 04), and optimize and prefer words with two or less duplicate letters (strategy 05) performed so much better than the other optimize* strategies because of the lack of letter frequency soft constraints.
Time to solve single puzzle (seconds) by strategy
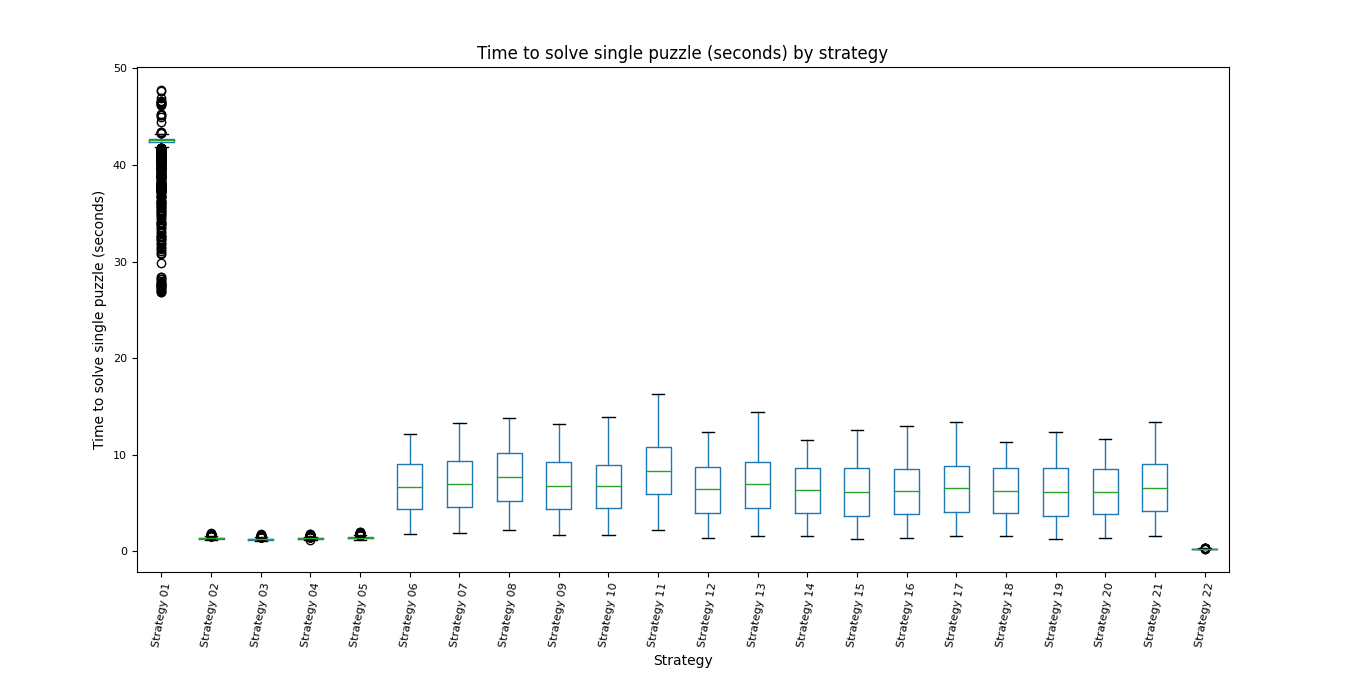
- The analysis in the Simulation time (hours) by strategy section applies here as well. No other remarkable comments to make.
Top 10 most frequently guessed words over all strategies
Word | Count | Frequency |
sayne | 9266 | 3.72% |
oater | 5716 | 2.30% |
semee | 4614 | 1.85% |
sycee | 4611 | 1.85% |
roate | 4296 | 1.73% |
orate | 4133 | 1.66% |
handy | 2365 | 0.95% |
crump | 2337 | 0.94% |
glove | 2334 | 0.94% |
swift | 2333 | 0.94% |
Strategy 01
Top 10 most frequency guessed words for Strategy 01
Word | Count | Frequency |
intro | 10 | 0.09% |
ethic | 9 | 0.08% |
raggy | 8 | 0.07% |
email | 8 | 0.07% |
extra | 8 | 0.07% |
itchy | 8 | 0.07% |
radix | 7 | 0.06% |
redan | 7 | 0.06% |
rayah | 7 | 0.06% |
remen | 7 | 0.06% |
Strategy 02
Top 10 most frequency guessed words for Strategy 02
Word | Count | Frequency |
twain | 6 | 0.05% |
piing | 6 | 0.05% |
lunch | 6 | 0.05% |
vying | 6 | 0.05% |
sassy | 6 | 0.05% |
tepee | 6 | 0.05% |
sheen | 6 | 0.05% |
state | 5 | 0.04% |
jiver | 5 | 0.04% |
smash | 5 | 0.04% |
Strategy 03
Top 10 most frequency guessed words for Strategy 03
Word | Count | Frequency |
druxy | 39 | 0.36% |
abhor | 35 | 0.32% |
bortz | 34 | 0.31% |
abort | 28 | 0.26% |
ablow | 25 | 0.23% |
blowy | 21 | 0.19% |
adept | 19 | 0.17% |
empty | 16 | 0.15% |
chivy | 15 | 0.14% |
deoxy | 12 | 0.11% |
Strategy 04
Top 10 most frequency guessed words for Strategy 04
Word | Count | Frequency |
ripes | 69 | 0.62% |
rioja | 60 | 0.54% |
rings | 54 | 0.49% |
riots | 51 | 0.46% |
rimus | 50 | 0.45% |
riped | 50 | 0.45% |
rinks | 48 | 0.43% |
rines | 48 | 0.43% |
rindy | 45 | 0.40% |
rinds | 40 | 0.36% |
Strategy 05
Top 10 most frequency guessed words for Strategy 05
froth | 6 | 0.05% |
tsade | 6 | 0.05% |
scrae | 6 | 0.05% |
sleep | 6 | 0.05% |
slung | 6 | 0.05% |
tutor | 6 | 0.05% |
plush | 6 | 0.05% |
aalii | 6 | 0.05% |
extra | 6 | 0.05% |
outgo | 6 | 0.05% |
Strategy 06
Top 10 most frequency guessed words for Strategy 06
Word | Count | Frequency |
resee | 1448 | 11.47% |
eerie | 862 | 6.83% |
taata | 533 | 4.22% |
araba | 265 | 2.10% |
ovolo | 212 | 1.68% |
alate | 153 | 1.21% |
asana | 147 | 1.16% |
satai | 98 | 0.78% |
arret | 79 | 0.63% |
aecia | 57 | 0.45% |
Strategy 07
Top 10 most frequency guessed words for Strategy 07
Word | Count | Frequency |
oater | 995 | 9.21% |
orate | 692 | 6.41% |
roate | 567 | 5.25% |
lysin | 189 | 1.75% |
aisle | 75 | 0.69% |
nails | 61 | 0.56% |
elsin | 57 | 0.53% |
nirls | 56 | 0.52% |
anils | 55 | 0.51% |
slice | 48 | 0.44% |
Strategy 08
Top 10 most frequency guessed words for Strategy 08
Word | Count | Frequency |
oater | 1137 | 10.59% |
orate | 580 | 5.40% |
roate | 537 | 5.00% |
lysin | 190 | 1.77% |
aisle | 77 | 0.72% |
nirls | 60 | 0.56% |
toils | 58 | 0.54% |
nails | 55 | 0.51% |
noils | 54 | 0.50% |
slain | 47 | 0.44% |
Strategy 09
Top 10 most frequency guessed words for Strategy 09
Word | Count | Frequency |
areae | 2307 | 18.99% |
lotto | 471 | 3.88% |
taboo | 232 | 1.91% |
looey | 141 | 1.16% |
rotor | 128 | 1.05% |
soote | 126 | 1.04% |
retro | 122 | 1.00% |
simis | 104 | 0.86% |
trior | 92 | 0.76% |
haole | 78 | 0.64% |
Strategy 10
Top 10 most frequency guessed words for Strategy 10
Word | Count | Frequency |
oater | 869 | 8.01% |
roate | 758 | 6.99% |
orate | 682 | 6.29% |
lysin | 194 | 1.79% |
nails | 64 | 0.59% |
aisle | 60 | 0.55% |
nirls | 57 | 0.53% |
slice | 49 | 0.45% |
toils | 47 | 0.43% |
aloin | 43 | 0.40% |
Strategy 11
Top 10 most frequency guessed words for Strategy 11
Word | Count | Frequency |
oater | 916 | 8.49% |
orate | 722 | 6.69% |
roate | 671 | 6.22% |
lysin | 194 | 1.80% |
aisle | 67 | 0.62% |
nails | 58 | 0.54% |
nirls | 56 | 0.52% |
slice | 54 | 0.50% |
anils | 50 | 0.46% |
toils | 47 | 0.44% |
Strategy 12
Top 10 most frequency guessed words for Strategy 12
Word | Count | Frequency |
oater | 891 | 8.22% |
orate | 730 | 6.74% |
roate | 688 | 6.35% |
lysin | 194 | 1.79% |
nails | 64 | 0.59% |
aisle | 64 | 0.59% |
anils | 59 | 0.54% |
nirls | 56 | 0.52% |
noils | 53 | 0.49% |
slice | 51 | 0.47% |
Strategy 13
Top 10 most frequency guessed words for Strategy 13
oater | 888 | 8.19% |
roate | 721 | 6.65% |
orate | 700 | 6.46% |
lysin | 194 | 1.79% |
aisle | 69 | 0.64% |
anils | 60 | 0.55% |
slice | 58 | 0.54% |
nirls | 57 | 0.53% |
nails | 57 | 0.53% |
toils | 46 | 0.42% |
Strategy 14
Top 10 most frequency guessed words for Strategy 14
Word | Count | Frequency |
semee | 2304 | 18.73% |
gayly | 749 | 6.09% |
fayre | 203 | 1.65% |
sassy | 191 | 1.55% |
hayey | 174 | 1.41% |
poori | 148 | 1.20% |
feyly | 117 | 0.95% |
lassy | 114 | 0.93% |
cooer | 104 | 0.85% |
thymy | 101 | 0.82% |
Strategy 15
Top 10 most frequency guessed words for Strategy 15
Word | Count | Frequency |
sayne | 2302 | 21.45% |
mohur | 219 | 2.04% |
goier | 209 | 1.95% |
boart | 151 | 1.41% |
forte | 128 | 1.19% |
borty | 108 | 1.01% |
hoaed | 81 | 0.75% |
sohur | 76 | 0.71% |
roate | 66 | 0.61% |
paoli | 65 | 0.61% |
Strategy 16
Top 10 most frequency guessed words for Strategy 16
Word | Count | Frequency |
sayne | 2302 | 21.50% |
mohur | 219 | 2.05% |
goier | 208 | 1.94% |
boart | 148 | 1.38% |
forte | 125 | 1.17% |
borty | 109 | 1.02% |
hoaed | 80 | 0.75% |
sohur | 77 | 0.72% |
roate | 66 | 0.62% |
porin | 66 | 0.62% |
Strategy 17
Top 10 most frequency guessed words for Strategy 17
Word | Count | Frequency |
sycee | 2293 | 19.75% |
laari | 465 | 4.00% |
gayly | 196 | 1.69% |
maare | 184 | 1.58% |
baaed | 154 | 1.33% |
salsa | 145 | 1.25% |
reata | 140 | 1.21% |
craal | 136 | 1.17% |
tassa | 77 | 0.66% |
wooer | 73 | 0.63% |
Strategy 18
Top 10 most frequency guessed words for Strategy 18
Word | Count | Frequency |
semee | 2309 | 18.79% |
gayly | 753 | 6.13% |
fayre | 205 | 1.67% |
sassy | 200 | 1.63% |
hayey | 174 | 1.42% |
poori | 155 | 1.26% |
lassy | 119 | 0.97% |
feyly | 119 | 0.97% |
cooer | 104 | 0.85% |
thymy | 103 | 0.84% |
Strategy 19
Top 10 most frequency guessed words for Strategy 19
Word | Count | Frequency |
sayne | 2309 | 21.55% |
mohur | 227 | 2.12% |
goier | 209 | 1.95% |
boart | 156 | 1.46% |
forte | 134 | 1.25% |
borty | 115 | 1.07% |
hoaed | 81 | 0.76% |
sohur | 78 | 0.73% |
porin | 66 | 0.62% |
roate | 66 | 0.62% |
Strategy 20
Top 10 most frequency guessed words for Strategy 20
Word | Count | Frequency |
sayne | 2309 | 21.56% |
mohur | 227 | 2.12% |
goier | 209 | 1.95% |
boart | 156 | 1.46% |
forte | 134 | 1.25% |
borty | 115 | 1.07% |
hoaed | 81 | 0.76% |
sohur | 78 | 0.73% |
roate | 66 | 0.62% |
porin | 66 | 0.62% |
Strategy 21
Top 10 most frequency guessed words for Strategy 21
Word | Count | Frequency |
sycee | 2309 | 19.91% |
laari | 468 | 4.03% |
gayly | 197 | 1.70% |
maare | 186 | 1.60% |
craal | 171 | 1.47% |
baaed | 155 | 1.34% |
salsa | 146 | 1.26% |
reata | 140 | 1.21% |
tassa | 80 | 0.69% |
wooer | 74 | 0.64% |
Strategy 22
Top 10 most frequency guessed words for Strategy 22
Word | Count | Frequency |
handy | 2309 | 19.39% |
swift | 2308 | 19.38% |
glove | 2307 | 19.37% |
crump | 2306 | 19.36% |
stake | 3 | 0.03% |
rupee | 2 | 0.02% |
snipe | 2 | 0.02% |
piker | 2 | 0.02% |
repel | 2 | 0.02% |
topic | 2 | 0.02% |
Conclusion
In this case study we first introduced what Wordle is, how to play the game, what Z3 is, and what SMT is. Next we described the steps to transcribe the rules of Wordle into a mathematical formula that can be leveraged by the Z3 SMT solver. Then we explained the various Wordle solving strategies we were going to have Z3 run simulations over. Finally we presented the results of the Z3 Wordle solving simulations.
Appendix
Solver (Strategy 01) raw results (csv)
Optimize (Strategy 02) raw results (csv)
Optimize and prefer words with no duplicate letters (Strategy 03) raw results (csv)
Optimize, prefer words with no duplicate letters, and prefer words with two or less duplicate letters (Strategy 04) raw results (csv)
Optimize and prefer words with two or less duplicate letters (Strategy 05) raw results (csv)
Optimize with letter frequency from total list (Strategy 06) raw results (csv)
Optimize with letter frequency from total list and prefer words with no duplicate letters (Strategy 07) raw results (csv)
Optimize with letter frequency from total list, prefer words with no duplicate letters, and prefer words with two or less duplicate letters (Strategy 08) raw results (csv)
Optimize with letter frequency from total list and prefer words with two or less duplicate letters (Strategy 09) raw results (csv)
Optimize with letter frequency from answer list (Strategy 10) raw results (csv)
Optimize with letter frequency from answer list and prefer words with no duplicate letters (Strategy 11) raw results (csv)
Optimize with letter frequency from answer list , prefer words with no duplicate letters, and prefer words with two or less duplicate letters (Strategy 12) raw results (csv)
Optimize with letter frequency from answer list and prefer words with two or less duplicate letters (Strategy 13) raw results (csv)
Optimize with letter position frequency from total list (Strategy 14) raw results (csv)
Optimize with letter position frequency from total list and prefer words with no duplicate letters (Strategy 15) raw results (csv)
Optimize with letter position frequency from total list, prefer words with no duplicate letters, and prefer words with two or less duplicate letters (Strategy 16) raw results (csv)
Optimize with letter position frequency from total list and prefer words with two or less duplicate letters (Strategy 17) raw results (csv)
Optimize with letter position frequency from answer list (Strategy 18) raw results (csv)
Optimize with letter position frequency from answer list and prefer words with no duplicate letters (Strategy 19) raw results (csv)
Optimize with letter position frequency from answer list, prefer words with no duplicate letters, and prefer words with two or less duplicate letters (Strategy 20) raw results (csv)
Optimize with letter position frequency from answer list and prefer words with two or less duplicate letters (Strategy 21) raw results (csv)
Norvig (Strategy 22) raw results (csv)
References:
[1] https://www.nytimes.com/games/wordle/index.html
[2] https://github.com/Z3Prover/z3
[3] https://en.wikipedia.org/wiki/Satisfiability_modulo_theories
[4] https://typon.github.io/wordle.html
[5] https://z3prover.github.io/api/html/classz3py_1_1_solver.html
[6] https://z3prover.github.io/api/html/classz3py_1_1_optimize.html
[7] https://theory.stanford.edu/~nikolaj/programmingz3.html#sec-optimization
[8] https://github.com/norvig/pytudes/blob/main/ipynb/Wordle.ipynb
